Link Search Menu Expand Document
Radiance: A JS Ray Tracer

4: Shapes

Download code
04-shapes.zip
Live example
examples/04-shapes/index.html

In section 3, we created a ray-tracing engine that can render empty scenes. Which doesn’t sound like much, but along the way we’ve laid the foundations that’ll make the next part of the workshop much more straightforward.

In this section, we’ll add some colored spheres to our renderer. For now, they’ll appear as flat brightly-colored discs – this is fine; it’ll let us test our shape intersection code before we start adding effects like shading and reflection in the next section.

Number.EPSILON and rendering thresholds

“JavaScript arithmetic is Wobbly. It’s good arithmetic, but it Wobbles and the numbers get in the wrong places.”

​ – Winnie the Pooh (probably).

Ray-tracing uses lots of complex floating-point arithmetic, and floating-point arithmetic isn’t exact. The best we can guarantee is a very, very close approximation. Try running this in a JavaScript console:

> 0.1 + 0.2
< 0.30000000000000004

> (0.1 + 0.2) - 0.3 == 0
< false

To render a scene in our ray-tracer, we’ll need to run hundreds of calculations checking whether various rays intersect with different shapes and surfaces; these are done using floating-point arithmetic, and we’re often checking for a result that, in a perfect world, would equal zero. But as we’ve seen, we can’t count on getting exact results from the JS arithmetic engine.

We’re going to create a base class called Shape - all the shapes we use in our scenes will extend Shape. Create a new file called modules/shape.js with this content:

// modules/shape.js

import { THRESHOLD } from './settings.js';

export class Shape {

    constructor(color) {
        this.color = color;
    }

    intersect = () => { throw ("Classes which extend Shape must implement intersect"); };

    closestDistanceAlongRay = (ray) => {
        let distances = this.intersect(ray).filter(d => d > THRESHOLD);
        let shortestDistance = Math.min.apply(Math, distances);
        return shortestDistance;
    }
}

For now, shapes in our world have only one responsibility: we can pass a ray of light into the shape and say “hey, does this ray intersect you anywhere?” – and if it does, what’s the distance from the start of the ray to the nearest intersection point?

Because we know the starting point of every ray, and the direction it’s pointing, if we know the distance along that ray where it intersects the shape, we can calculate the exact point in space where that ray intersects that shape.

The sphere

The first shape we’re going to add to our system is the sphere.

Here’s the code: put this in modules/shapes/sphere.js:

// modules/shapes/sphere.js

import { Shape } from '../shape.js';
import { Vector } from '../vector.js';

export class Sphere extends Shape {
    constructor(center, radius, color) {
        super(color);
        this.center = center;
        this.radius = radius;
    }

    intersect = ray => {
        // Offset - the position of the sphere relative to the start of the ray
        let os = Vector.from(this.center).to(ray.start);

        // Calculate a,b,c so we can plug them into the quadratic formula. Except
        // a should be the squared Euclidian distance of the ray direction,
        // but ray directions are normalised to a unit vector, so a will be 1, 
        // so we can ignore it.
        let b = 2 * os.dot(ray.direction);
        let c = os.squid - this.radius * this.radius;
        
        let discriminant = b * b - 4 * c;

        // If b^2-4ac is negative, the ray never intersects the sphere.
        // Math nerds: that means the quadratic equation has complex solutions ;)
        if (discriminant < 0) return [];

        // If the root is zero, the ray touches the surface of the sphere
        // but doesn't actually go through it, so there is only one intersection.        
        if (discriminant == 0) return [-b / 2 ];

        // Otherwise we have two intersections - one on the way in, one on the way out.
        let root = Math.sqrt(discriminant);
        return [ (-b - root) / 2, (-b + root) / 2 ];
    };
}

All the sphere actually needs to do is override the intersect method from the Shape base class, and provide the code that’ll find intersections between a ray travelling through space, and the surface of a sphere. Each ray will intersect the sphere in zero, one, or two places.

The intersections here are the roots of a quadratic equation - the thing you probably learned in high school and though you’d never use again. Just in case you’ve forgotten, here’s the Quadratic Formula Kitten to remind you:

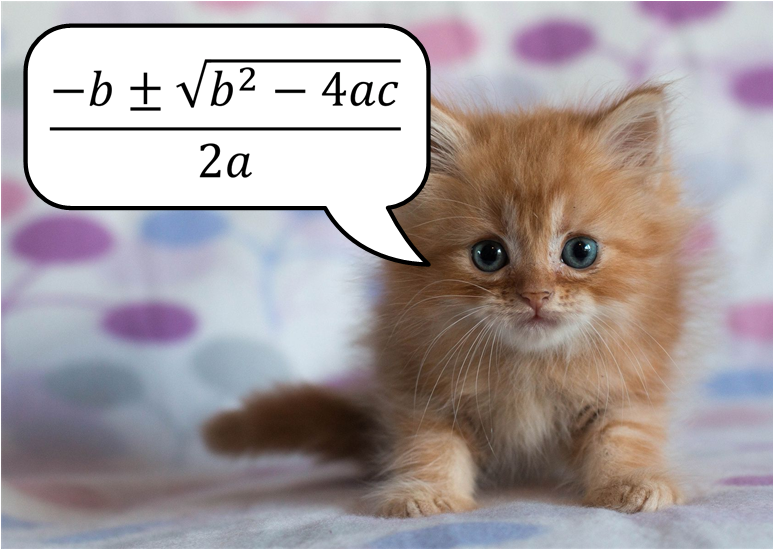
image-20220319164818563

So we do some arithmetic sleight-of-hand to turn our sphere into those three values a, b, c, then we plug the whole thing into the quadratic formula and see how many solutions we get.

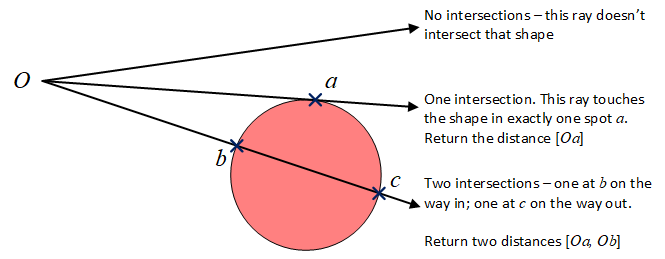
image-20220319161740559

The important bit is that it’ll give us an array of distances. If the ray doesn’t intersect the sphere, we get back an empty array. If the ray just grazes the surface of the sphere, we get a single intersection, and return a single distance; and if the ray goes through the sphere, we get two intersection points.

Now, we’ll modify the trace method on our Ray object to look for these intersections:

trace = (scene) => {
    let distances = scene.shapes.map(s => s.closestDistanceAlongRay(this));
    let shortestDistance = Math.min.apply(Math, distances);
    if (shortestDistance == Infinity) return scene.background;
    let nearestShape = scene.shapes[distances.indexOf(shortestDistance)];
    return nearestShape.color;
}

Adding shapes to a scene

When we create a Scene, we’ll pass in an array of shapes. Modify modules/scene.js so it looks like this:

// modules/scene.js

import { Color } from './color.js';

export class Scene {
    constructor(camera, background, shapes) {
        this.camera = camera;
        this.background = background ?? Color.Black;
        this.shapes = shapes ?? [];
    }
    trace = (x, y) => this.camera.trace(this, x, y);
}

Now we’ll modify main.js to create some spheres and add them to our scene:

// main.js

import { Renderer } from './modules/renderer.js';
import * as ExampleScenes from './scenes/examples.js';

let canvas = document.getElementById('my-canvas');
let ctx = canvas.getContext('2d');
let renderer = new Renderer(canvas.width, canvas.height);

function paintPixel(x, y, color) {  
  ctx.fillStyle = color.html;
  ctx.fillRect(x, y, 1, 1);
}

let scene = ExampleScenes.ColoredSpheres();
renderer.render(scene, paintPixel);

If it worked? You’ll get this - five colored circles.

image-20220319234731133

The important thing to notice here is that even though we’re just rendering them as flat discs, our ray tracer is smart enough to know which bits we can see, and which bits are hidden behind another shape.

Download code
04-shapes.zip
Live example
examples/04-shapes/index.html